Cours 3

(niveau de base)

Instant philo

Je rédigerais quand j’aurais 5mn. Problèmes de biais dans les bases (?)

Apprentissage par optimisation

La plupart des véritables algorithmes de machine learning sont de cette catégorie. Pour vous expliquer ce que c’est, je vais me servir d’un exemple.

On reprend le problème de séparation hommes / femme, avec comme caractéristiques : [taille, poids].

Je veux construire un algorithme qui va trouver la meilleure droite pour séparer ces deux classes. Je sais de plus que cette droite passe par le point M marqué en noir dans la figure suivante.

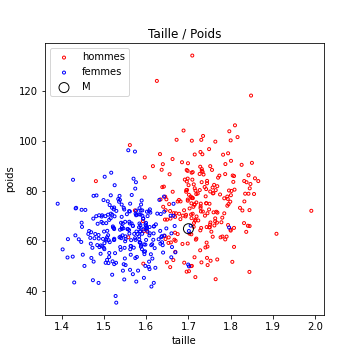
nuage de points et M

L’équation de n’importe quelle droite (non verticale) passant par ce point (M[0],M[1]) est donc \(y - p(x-M[0]) -M[1] = 0\), avec \(p \in R\)

Pour un paramètre p fixé (donc pour une droite donnée), si le vecteur de caractéristiques est [x,y], la décision de notre algorithme est prise de la façon suivante :

La figure suivante présente 2 exemples de droites (donc deux algorithmes différents mais basés sur ce principe), dont les performances en Apprentissage sont différentes

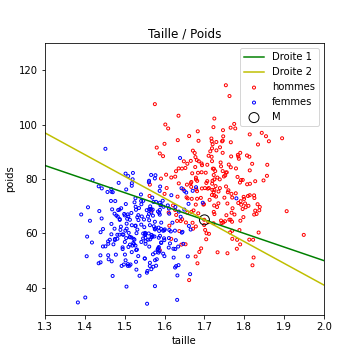
deux droites de séparation

Posez vous les questions suivantes :

Il s’agit donc de trouver le paramètre p qui donne les meilleurs résultats. Meilleurs signifiant ici : avec la meilleure mesure de performance en apprentissage. C’est un problème d’optimisation. Vous avez eu des cours à ce sujet, je pense.

La solution la plus simple pour trouver une “bonne” solution consiste à faire la chose suivante (en pseudo code)

# On se donne une situation de départ
testp = -50

# On cree une variable pour mémoriser les meilleurs performances trouvées
bestPerreur = 1

# On crée une variable pour fixer le nombre d'essais maximum
nMax= 1000

# On crée une variable pour compteur les tests déja faits
n=0

# Puis on va chercher des meilleurs solutions.
while n < nMax:

  # on mesure les perf obtenues sur la base d'apprentissage avec ces paramètres.
  newPerreur = mesureProbaErreur(testp, baseApprentissage)

  # On met a jour les meilleurs perf trouvées et les meilleurs param trouvés
  if newPerreur < bestPerreur :
    p = testp
    bestPerreur = newPerreur

  # On génère une nouvelle configuration en deplacant testp
  # UN PETIT PEU et AU HASARD !
  testp+= random.random() *pas

  n+=1

Mon pseudo code fonctionne en python (sous réserve d’avoir fait la fonction mesureProbaErreur). A ceci près que je n’ai pas fixé de valeur à la variable pas… Cette variable s’appelle le pas de la descente.

A l’issue de cet algorithme :

Pour mieux comprendre la partie descente stochastique et cette histoire de pas de la descente, vous pourriez aller voir la page sur la descente stochastique qui contient notamment un lien vers du code exécutable (sur un exemple plus simple) que vous pourrez exécuter, modifier…

Pour information, voici les résultats trouvés sur ce jeu de test par cet algo :

pente : -177.35109477634492
proba d erreur : 0.086

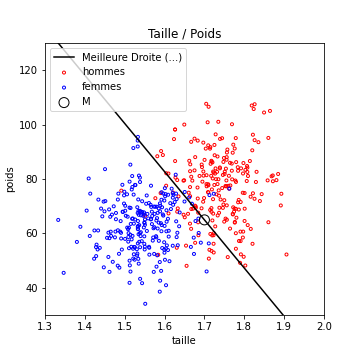
meilleur droite trouvée

Cet algo fonctionne !

La bonne nouvelle, c’est que vous pouvez aller le tester. Je vous recommande d’essayer de changer le pas, nMax voir ce que cela change (et de comprendre pourquoi)…

Recherche de plus d’un paramètre

Le mode de fonctionnement est très similaire si l’algorithme travaille avec plus d’un paramètre.

Imaginons que je ne sache pas placer le point M. Les droites que je cherche ont pour équation par y - px -b = 0. Je cherche donc le meilleur couple (p,b).

Sauriez vous adapter l’algo précédent ?

Il suffit, en gros, de changer :

Cette méthode simple mais efficace rentre dans la grande catégorie des algorithmes d’optimisation qui servent à peu près à tout (notamment à trouver les poids d’un réseau de neurones, réseaux que nous verrons dans le cours 4).

Pour information, l’algo que nous avons vu fait partie de la classe des algorithmes dits “de Monte carlo”. Le paramètre pas de la descente évoqué dans notre exemple se retrouve dans toutes ces méthodes, sous une forme ou une autre. Il faut souvent l’adapter au problème traité.

Évolution des performances pendant l’apprentissage

On voit dans le pseudo code qui précède, que l’algo va en fait voir la totalité de la base de nombreuses fois (1000 fois)

Au fur et à mesure des essais, la probabilité d’erreur devrait diminuer. Dit autrement, la précision en apprentissage doit augmenter avec le temps, pendant l’apprentissage.

Elle doivent (si tout se passe bien) évoluer de la façon suivante :

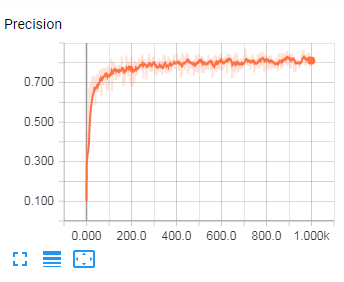
exemple de proba d'erreur en apprentissage

La figure précédente est en fait tirée des tests effectués par l’un d’entre vous sur de la reconnaissance de caractères à partir d’images (à l’aide d’un réseau de neurones). Il y a 10 classes possibles, l’algorithme a donc, en tirant au hasard sa réponse, une probabilité de succès de 0.1. Ce sont les performances au début de l’apprentissage. On voit qu’il progresse, puis stagne.

On voit que notre algorithme a atteint, à la fin de son apprentissage, une précision en apprentissage d’à peu près 0.80. La valeur finale est peu importante (elle dépend de la qualité de l’algorithme et de la difficulté du problème). Par contre, on voit qu’il ne sert plus à rien de continuer à entraîner cet algorithme, il a déjà atteint ses limites depuis longtemps.

Je vous rappelle que ces performances ne sont toutefois pas une évaluation correcte de ce que ferait notre algorithme en situations réelles, car il est ici évalué sur des exemples qu’il connaît déjà.

On doit donc mesurer maintenant sa probabilité de classification correcte sur la base de généralisation.

Dans le cas correspondant à l’image présentée au dessus dessus, la probabilité de classification correcte en généralisation était de 0.76.

TODO plus tard :

Vous pouvez passer au Cours 4 ou repartir vers le Sommaire ___